炒炒剩饭。用K大侠的解推广万大侠的三等分面积题(改正了一个计算错误）

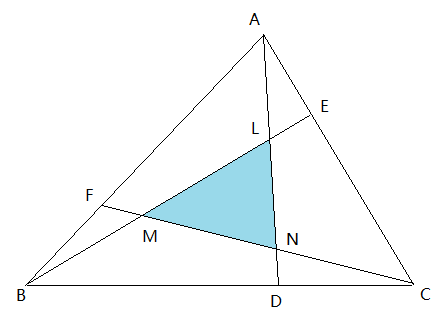
题。如上图。E，F，D分别是三边上的n（n>2）等分点。即AE:EA=AF:FB=BD:DC=(n-1):1.已知三角形ABC的面积。求三角形LMN的面积。

解：S_LMN = (n-2)^2/(n^2-n+1)*S_ABC

下面的推理全盘照搬K大侠的解。请大家检验。原题有多种解。其它的解法能不能推广？

利用梅涅劳斯(Menelaus)定理
设 BM:ML:LE = a:b:c
则对三角形ABE和直线FC用梅氏定理,有
 BM/ME * EC/CA * AF/FB = 1
即  a/(b+c) * (n-1)/n * (n-1)/1 = 1
  a/(b+c) = n/((n-1)^2 )   ---- (1)

再对三角形BCE和直线DA用梅氏定理，有
  BD/DC * CA/AE * EL/LB= 1
  (n-1)/1 * n/1 * c/(a+b) = 1
  c/(a+b) = 1/(n(n-1))          --- (2)
 
由（1),(2)可解出 a:b:c = n:n(n-2):1
同理可得
  AL:LN:ND = CN:NM:MF = BM:ML:LE = a:b:c = n:n(n-2):1
 
于是 S_LMN = LM/BL * S_BNL
          = LM/BL * NL/OL * S_BDL
          = LM/BL * NL/OL * DL/AD * S_ABD
          = LM/BL * NL/OL * DL/AD * BD/BC * S_ABC
          = b/(a+b) * b/(b+c) * (b+c)/(a+b+c) * (n-1)/n * S_ABC
          = b^2/((a+b)(a+b+c)) * (n-1)/n * S_ABC
          = (n(n-2))^2/（n+n(n-2))(a+b+c) * (n-1)/n* S_ABC
          = (n-2)^2/(a+b+c) * S_ABC
          = (n-2)^2/(n^2-n+1)*S_ABC